Skip to main content

Binary Tree Questions 二叉树问题

Yujie LiuAbout 6 minComputer ScienceAlgorithmsLeetcodeBinary Tree

Binary Tree Questions 二叉树问题

This article is concluded from this articleopen in new window in Chinese.

Cheatsheet: Steps to solve binary tree questions

  1. Can we get the answer by traversing the binary tree once? 是否能通过遍历一棵树来获取结果？
  2. If not, can we define a recursive function that gets the answer to the original question from the answer to the subtree? If the solution involved the information of the subtree, it is recommended to use post-order position to handle data. 如果不能，是否能通过递归的方式获取子树的结果，再根据子树的结果计算最终结果。通常而言，由于需要子树的结果，常在后序位置处理节点数据。
  3. No matter which model you are using, we need to think about what and when should we do for a single node? (Pre/In/Post-order) 无论使用哪一种思维模式，都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做

Thinking models for binary tree questions

There are only two models for binary tree questions:

  1. Can we get the answer by traversing the tree? If yes, we can define a traverse function along with external variables to solve the question.
  2. Can we define a recursive function, using the answers of sub-trees to get the final answer? If yes, we can define this recursive function and use the return value to get the final answer.

No matter which model you are using, there are always one thing needs to think about:

  • Singled out a node of the binary-tree, what does we need to do? when should we do it? (Pre/In/Post-order)

A lot of questions can be abstracted into the binary tree problems, for example, the quick sort and the merge sort

  1. Quick sort: Pre-order iteration of a binary tree
void sort(int[] nums, int lo, int hi) {

    // Pre-order: swap the elements to get the pivot element p
    int p = partition(nums, lo, hi);

    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}
  1. Merge sort: Post-order iteration of a binary tree
void sort(int[] nums, int lo, int hi) {
    int mid = (lo + hi) / 2;
    // sort nums[lo..mid]
    sort(nums, lo, mid);
    // sort nums[mid+1..hi]
    sort(nums, mid + 1, hi);

    // Post-order: merge the nums[lo..mid] and the nums[mid+1..hi]
    merge(nums, lo, mid, hi);
}

Understanding of Pre/In/Post-order traversal

Basic Concept

class TreeNode {
    int val;
    TreeNode left, right;
}

void traverse(TreeNode root) {
		if (root == null) {
      	return;
    }
    
  	//Pre-order
    traverse(root.left);
  	//In-order
    traverse(root.right);
  	//Post-order
}

These are the methods to traverse the binary tree, which can be interpreted as a "Binary linked list". As shown in my blog Data Structure, we have two ways to traverse an array or linked list: Iteration and Recursion. Iterating a binary tree is much harder, so we usually written it in recursion format.

Three different position for handling data

Pre/In/Post-order are three different positions for handling the data of each node

  1. Pre-order: We just go into a node.
  2. Post-order: We have traversed all the nodes
  3. In-order: We have traversed the nodes from the left side, and prepare to do so for the right side.

Therefore, we only need to think about what should we do for each node, and select a traversal method to do the other jobs.

Why post-order traversal is special?

Before talking about the post-order traversal, let's firstly explains the pre-order and in-order traversals.

  • Pre-order: Not special. We just habitually handle the order-insensitive data in pre-order position
  • In-order: Typically used in BFS

We may notice that the code in the pre-order position can only get the data passed from the parent node from the function parameters, while the code in the post-order position can not only get the parameter data, but also the data from the sub-trees through the function return value.

This difference lead to two different solutions to two different questions, for example:

  1. How to print the level of each node?
  2. How to print the number of sub-tree nodes for each node?

The first question can be directly solved by passing the level number from the parent function, while the second one needs the data from the sub-trees, so we have two different solutions:

  1. Questions 1
void traverse(TreeNode root, int level) {
    if (root == null) {
        return;
    }
    // Pre-order position
    printf("Node %s is at %d level", root, level);
    traverse(root.left, level + 1);
    traverse(root.right, level + 1);
}

traverse(root, 1);
  1. Question 2
int count(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int leftCount = count(root.left);
    int rightCount = count(root.right);
    // Post-order
    printf("Node %s 's left sub-tree has' %d nodes，right sub-tree has %d nodes", root, leftCount, rightCount);

    return leftCount + rightCount + 1;
}

Therefore, if the calculations need the data from the sub-trees, we typically need to use the post-order traversal to handle the data.

Examples of two thinking models

T104. Maximum Depth of Binary Treeopen in new window

Given the root of a binary tree, return its maximum depth.

A binary tree's maximum depth is the number of nodes along the longest path from the root node down to the farthest leaf node.

Example 1:

img
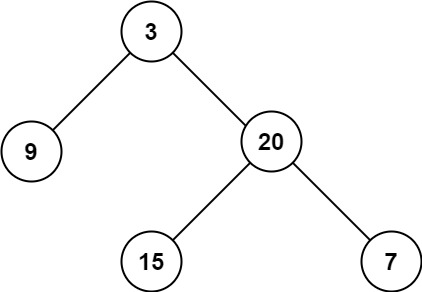
Input: root = [3,9,20,null,null,15,7]
Output: 3

Example 2:

Input: root = [1,null,2]
Output: 2

Constraints:

  • The number of nodes in the tree is in the range [0, 104].
  • -100 <= Node.val <= 100

Iteration model

we can define a traverse() function along with external variables to solve the question.

class Solution {
  	//Record the depth of current node
    int depth = 0;
  	//Record the max depth
    int maxDepth = 0;
  
    public int maxDepth(TreeNode root) {
        traverse(root);
        return maxDepth;
    }

    private void traverse(TreeNode node) {
        if (node == null){
            return;
        }

        //Pre-order position: when reaching a node, depth++, compare the depth and maxDepth
        depth++;
        if (node.left == null && node.right == null){
            maxDepth = Math.max(depth, maxDepth);
        }

        traverse(node.left);
      	//In-order position: the update of maxDepth can also be put here
        traverse(node.right);

        //Post-order position: when leaving a node, depth--
        depth--;
    }
}

Recursive mindset

We can define a recursive function and use the return value to get the final answer. Since we are using the information of sub-trees, we typically handle the data for each node in post-order position.

int maxDepth(TreeNode root) {
	if (root == null) {
		return 0;
	}
  
	//Calculate the max depth of left sub-tree and right sub-tree
	int leftMax = maxDepth(root.left);
	int rightMax = maxDepth(root.right);
	
  //Post-order position: Max of left and right plus myself (+1)
	int res = Math.max(leftMax, rightMax) + 1;

	return res;
}

Understanding of Dynamic Programming, Backtracking and DFS algorithms under the framework of the binary tree

Let's firstly talk about the conclusions: The Dynamic Programming/DFS/Backtracking algorithms can all be viewed as extensions of the binary tree problem, except that their focus is different:

  • Dynamic Programming algorithm belongs to the idea of decomposition problem, its focus is on the whole "subtree".
  • The Backtracking algorithm belongs to the idea of traversal, and its focus is on the "branches" between nodes.
  • The DFS algorithm is a traversal algorithm that focuses on individual nodes.

Dynamic Programming

Count the number of sub-tree nodes using Dynamic Programming

int count(TreeNode root) {
    if (root == null) {
        return 0;
    }
    
    // We cares about the number of sub-tree nodes
    int leftCount = count(root.left);
    int rightCount = count(root.right);
    
    // Post-order position
    return leftCount + rightCount + 1;
}

Same story in Fibonacci

int fib(int N) {
    if (N == 1 || N == 2) return 1;
    return fib(N - 1) + fib(N - 2);
}

Backtracking

Firstly we think about the steps when traversing a binary tree

void traverse(TreeNode root) {
    if (root == null) return;
  
    printf("From node %s to %s", root, root.left);
    traverse(root.left);
    printf("From %s back to node %s", root.left, root);

    printf("From node %s to node %s", root, root.right);
    traverse(root.right);
    printf("From node %s back to %s", root.right, root);
}

Easy right? Then we can talk about a generic tree or N-ary tree.

class Node {
    int val;
    Node[] children;
}

void traverse(Node root) {
    if (root == null) return;
    for (Node child : root.children) {
        printf("From node %s to node %s", root, child);
        traverse(child);
        printf("From node %s back to node %s", child, root);
    }
}

Based on this, we can extend it to the framework of Backtracking algorithms

void backtrack(...) {
    for (int i = 0; i < ...; i++) {
        // Making a choice
        ...

        // Goes to the next level of decision tree
        backtrack(...);

        // Undo the choice
        ...
    }
}

We can conclude that the backtracking always focus on moving among nodes, which can be interpreted as the "branches" in the binary trees

DFS

Self-increase 1 for each node of a binary tree. This is the simplest question using DFS algorithm.

void traverse(TreeNode root) {
    if (root == null) return;
    // Plus one for each node
    root.val++;
    
    traverse(root.left);
    traverse(root.right);
}

See. We always focus on the nodes, same story for the nodes of a binary tree.

With this in mind, we can tell the difference between the DFS and Backtracking algorithms

// DFS: do and undo the choice outside the loop
void dfs(Node root) {
    if (root == null) return;
    // Make a choice
    print("I am at node %s", root);
  
    for (Node child : root.children) {
        dfs(child);
    }
  
    // Undo the choice
    print("I am leaving node %s", root);
}

// Backtracking: do and undo the choice inside the loop
void backtrack(Node root) {
    if (root == null) return;
    for (Node child : root.children) {
        // Make a choice
        print("I am at the branch from node %s to node %s", root, child)
        backtrack(child);
        // undo the choice
        print("I am leaving the branch from node %s to node %s", child, root)
    }
}

Level-order traversal (BFS) framework

void levelTraverse(TreeNode root) {
    if (root == null) return;
    Queue<TreeNode> q = new LinkedList<>();
    q.offer(root);

    // From top to down
    while (!q.isEmpty()) {
        int sz = q.size();
        // From left to right for each level
        for (int i = 0; i < sz; i++) {
            TreeNode cur = q.poll();
            // Put the nodes of next level into the queue
            if (cur.left != null) {
                q.offer(cur.left);
            }
            if (cur.right != null) {
                q.offer(cur.right);
            }
        }
    }
}
Last update:
Contributors: Yujie
A gift for my 23
Copyright © 2024 Yujie Liu